Extreme Risk Mitigation in Reinforcement Learning
In recent years, researchers have been leveraging reinforcement learning (RL) so that agents can refine specific behaviors. The behaviors of interest include the completion of intricate tasks, such as ensuring secure exploration or demonstrating risk-averse tendencies in unfamiliar environments. Our study seeks to design RL agents with an acute awareness of risk, particularly in scenarios that are characterized by exceedingly rare and extreme risks. In safety-critical applications, we naturally want to avoid undesirable states or returns that are fraught with risk. Risk quantification within the context of the learning agent thus plays a paramount role in the mitigation of catastrophic failures.
To illustrate this critical point, consider a vehicle that is traversing an unfamiliar freeway with an unknown speed limit. Faster speeds offer the advantage of expeditious arrival at one’s destination, but exceeding a certain speed threshold may occasionally result in fines — though incurring a fine is a very rare event. Consequently, a driver must modulate the vehicle’s speed to avoid penalties. The infrequency of such penalties complicates the development of risk-averse strategies.
An autonomous RL agent that is tasked with learning an optimal risk-averse policy in a scenario with such a rare penalty faces the formidable challenge of limited data availability. Traditional risk-averse RL algorithms grapple with two substantial limitations under these circumstances. First, they struggle to discern risks in scenarios with sparse data. Second, this inefficacy in risk detection yields high-variance estimates of the true risk measure (specifically the quantiles of the state-action value distribution). We propose an alternative approach that mitigates extreme risks by enhancing the modeling of the state-action value distribution. Our methodology hinges upon the use of extreme value theory (EVT) to model the tail region of the state-action value function’s quantile. EVT posits that the tail distribution adheres to a specific parametric form, which we propose to fit to the state-action value distribution in this context.
To address the issue of infrequent risk events and high-variance risk measure estimates, our proposed approach employs a parametric EVT-based distribution fitting procedure, which generates additional data points that constitute realizations of the state-action value distribution. Our tecHow does this methodology effectively address the challenge of limited data availability and high-variance risk measure estimation, particularly in the case of rare and high-risk events? The underlying rationale lies in the GPD distribution’s capacity to provide a subtle extrapolation into unobserved regions within the state-action value distribution’s support. This extrapolation is instrumental in reducing the variance of the risk measure and provides good risk mitigation strategies.hnique utilizes these newly acquired data points to iteratively update the state-action value distribution via the Bellman update operation. Within the framework of this research, we demonstrate that the quantile estimations of the state-action value distribution—computed with the proposed methodology—exhibit a reduced degree of variance, thus leading to lower-variance risk measure estimates. Finally, we conduct extensive empirical evaluations to assess the benefits of our proposed approach in risk mitigation and when modeling the tail quantiles of the state-action value distribution.
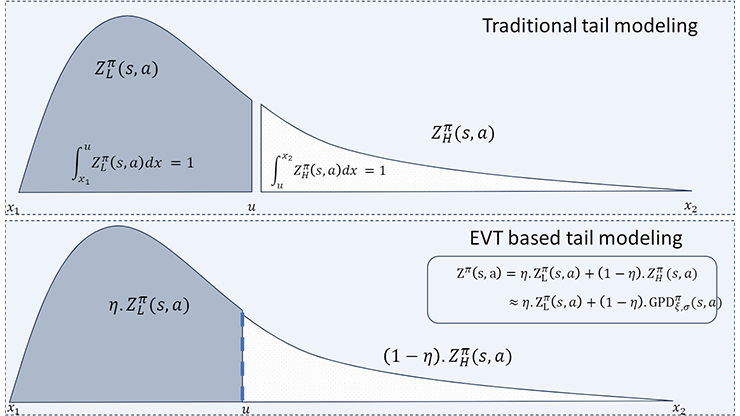
![<strong>Figure 1 .</strong> Modeling the tail and non-tail distributions of the state-action value function. The area under the non-tail distribution \(Z^{\pi}_L(s,a)\) and the tail distribution \(Z^{\pi}_H(s,a)\) is \(1\). Figure courtesy of [1].](/media/1ppowpet/figure1.jpg)
Consider a Markov decision process that is characterized by the tuple \((\mathcal{S}, \mathcal{A}, P_R, P_S, \gamma)\), where \(\mathcal{S}\) is the state space, \(\mathcal{A}\) is the action space, and \(P_R\) is the stochastic reward kernel such that \(P_R : \mathcal{S} \times \mathcal{A} \rightarrow \mathcal{P}(\mathcal{R})\); here, \(\mathcal{R}\) is the reward set. Furthermore, \(P_S : \mathcal{S} \times \mathcal{A} \rightarrow \mathcal{P}(\mathcal{S})\) is the probabilistic next state transition kernel and \(\gamma\) is the discount factor. The policy \(\pi\) of the agent is a mapping \(\pi : \mathcal{S} \rightarrow \mathcal{P}(\mathcal{A})\) and the future sum of discounted returns is a random variable that is denoted by \(J^{\pi}(s,a)=\Sigma^{\infty}_{t=0}\gamma^tR_t\), where \(R_t \sim P_R(S_t, A_t)\) and \(A_t \sim \pi(S_t)\), with \(S_0=s\) and \(A_0=a\). We denote the distribution that corresponds to the random variable \(J^{\pi}\) as \(Z^{\pi}\), and we denote the state-action value distribution of \((s,a)\) with \(Z^{\pi}(s,a)\).
The distributional Bellman equation updates the state-action value function distribution \(Z\) under policy \(\pi\):
\[T^{\pi}Z(s,a)=r(s,a)+\gamma\textrm{E}_{s'\sim P_S(s,a),a'\sim\pi(s')}Z(s',a'). \tag1 \]
The distribution function \(Z^{\pi}(s,a)\) characterizes the values that the random variable \(J^{\pi}(s,a)\) can assume. Knowledge of the distribution function \(Z^{\pi}(s,a)\) therefore helps us understand even the extreme values that \(J^{\pi}(s,a)\) may be assigned. We propose the use of EVT to approximate the extreme regions of \(Z^{\pi}(s,a)\). To characterize the distribution’s tail behavior, we invoke a particular theorem from EVT: the Pickands-Balkema-de Haan (PBD) theorem, whose formal expression asserts that the extreme values in a sequence of independent and identically distributed random variables converge to the generalized Pareto distribution (GPD). Let \(X_1 \cdots X_n\) be a sequence of independent and identically distributed random variables with a cumulative distribution function that is given by \(F\). According to the PBD theorem, we can approximate the conditional excess distribution \(F_u(x)=P(X-u \le x | X > u)\) via the GPD distribution with parameters \(\xi\), \(\sigma\).
For a sufficiently high given threshold \(u\), \(Z^{\pi}_L(s,a)\) denotes the non-tail distribution (see Figure 1). The subscript \(L\) signifies support values of \(Z^{\pi}\) that are lower than \(u\). Similarly, \(Z^{\pi}_H(s,a)\) denotes the tail distribution and the subscript \(H\) signifies the distribution with support values higher than \(u\). We assume that \(u\) is a sufficiently high threshold for the state-action pair \((s,a)\). The area under \(Z^{\pi}_H(s,a)\) is \(1\). We can hence obtain the state-action value distribution \(Z^{\pi}(s,a)\) by rescaling \(Z^{\pi}_H(s,a)\):
\[Z^{\pi}(s,a)=\eta Z^{\pi}_L(s,a)+(1-\eta)Z^{\pi}_H(s,a). \tag2\]
Given the new approximated tail distribution \(Z^{\pi}_H(s,a) \approx \textrm{GPD}\big(\xi(s,a),\sigma(s,a)\big)\), we propose the following modified Bellman equation:
\[T^{\pi}Z(s,a)=r(s,a)+\gamma\textrm{E}_{s'\sim P_S(s,a),a'\sim\pi(s')}\eta Z_L(s',a')+(1-\eta)Z_H(s',a'). \tag3\]
This EVT-based Bellman equation employs samples from the GPD distribution to update the current state-action value distribution \(Z(s,a)\). In order to fit the GPD distribution itself, we seek to obtain samples from \(Z_H(s,a)\) to update \(\xi(s,a)\), \(\sigma(s,a)\) through maximum likelihood estimation.
![<strong>Figure 2.</strong> Trajectories (in black) of an autonomous robot that must navigate from the small green circle to the larger blue circle; the area within the red circle has a minimal risk of penalties. <strong>2a.</strong> The baseline agent: a distributional soft actor critic. <strong>2b.</strong> Our proposed agent, which is risk averse and avoids the red circle. Figure courtesy of [1].](/media/xdvcclmj/figure2.jpg)
How does this methodology effectively address the challenge of limited data availability and high-variance risk measure estimation, particularly in the case of rare and high-risk events? The underlying rationale lies in the GPD distribution’s capacity to provide a subtle extrapolation into unobserved regions within the state-action value distribution’s support. This extrapolation is instrumental in reducing the variance of the risk measure and provides good risk mitigation strategies.
To illustrate the benefits of our proposed method in risk aversion and exemplify situations that are characterized by infrequent, high-risk occurrences, we examine a scenario in which an autonomous robot must navigate from a designated green circle to a specified blue circle. To replicate a situation with rare high-risk events, we introduce a red circle within which the agent is subjected to penalties, albeit with a minimal probability of only five percent. In principle, a risk-averse agent should steadfastly avoid this red region. But given the exceedingly low likelihood of penalty, a standard risk-averse agent may not be inclined to train a policy that avoids this area. In Figure 2, the trajectories of the baseline agent (a distributional soft actor critic) encroach into the red circle, while our proposed agent’s trajectories clearly avoid the risky red region.
More detailed explanations, proofs, and experimentation of complex, physics-based risky environments are available in our corresponding paper [1].
Karthik Somayaji coauthored a minisymposium presentation on this research at the 2023 SIAM Conference on Control and Its Applications, which took place in Philadelphia, Pa., last year.
References
[1] NS, K.S., Wang, Y., Schram, M., Drgona, J., Halappanavar, M., Liu, F., & Li, P. (2024). Extreme risk mitigation in reinforcement learning using extreme value theory. Trans. Mach. Learn. Res., 2835-8856.
About the Author
Karthik Somayaji
Ph.D. Student, University of California, Santa Barbara
Karthik Somayaji is a fourth-year Ph.D. student at the University of California, Santa Barbara. His research focuses on uncertainty quantification, language models, reinforcement learning, and machine learning (ML) applications to circuit design and optimization. Karthik is passionate about the integration of ML in industry and has interned at Intel and Siemens in this capacity. He is also a DAC Young Fellow.