Fighting Errors with Space
The fundamental unit in a quantum computer is a quantum bit (qubit), which is typically the state space of a microscopic particle such as a photon, ion, atom, etc. In quantum computing, qubits should be isolated from their surroundings to minimize noise. Yet by definition, the application of gates and measurements is a form of interaction between qubits and external observers; as such, any quantum computer is inevitably exposed to the environment. A quantum state may unfavorably change to another state at a particular point in time because of decoherence. Likewise, a quantum gate may not execute an operation exactly as intended due to technological limitations. These unwanted environmental interactions and operational imprecisions introduce errors to the system; a sufficient accumulation of errors can eradicate all useful information in a quantum state. To become practical, quantum computing must address the issue of errors.
In classical computation, an error is the flip of a bit between \(0\) and \(1\). In quantum computing, the analog of a bit flip is the Pauli \(X\) operator that switches between \(|0\rangle\) and \(|1\rangle\). Similarly, a phase flip error corresponds to the Pauli \(Z\) operator and multiplies the phase \(-1\) to \(|1\rangle\). More “violent” errors can also occur. For example, the environment may entangle with some qubits, evolve for some time, and finally disentangle by measuring itself out. For the purpose of this discussion, let us think of an error as an arbitrary linear operator. It may seem impossible to correct every error at first glance because of the uncountable possibilities. However, a theorem guarantees that if we can correct a set of errors, any operator in the vector space that is spanned by those errors can also be automatically corrected without extra effort. Therefore, correcting the Pauli \(X\), \(Y\), and \(Z\) errors sufficiently corrects all 1-qubit errors.
Much like the use of redundancy in classical error correction, a key principle of quantum error correction involves fighting errors with abundant space. Within a space \(\mathcal{H}\) of multiple physical qubits, we can choose a subspace \(\mathcal{L} \subset \mathcal{H}\) as the space of logical qubits. Typically, the dimension of \(\mathcal{H}\) is several magnitudes larger than that of \(\mathcal{L}\). The formulation of subspace \(\mathcal{L}\) should allow for the detection of an error that brings a state in \(\mathcal{L}\) to somewhere outside, and also permit the distinction of different errors. Error detection usually occurs via measurement, which should be just enough to infer the error without revealing the actual encoded state. Different errors must map \(\mathcal{L}\) to pairwise orthogonal subspaces in order to remain unambiguously distinguishable. An extension of this argument leads to the error correction condition: A set of errors \(\left\{E_{i}\right\}\) is correctable if and only if \(P E_{j}^{\dagger} E_{i} P=\alpha_{i j} P\) for any \(i, j,\) where \(\alpha_{i j}\) is a scalar and \(P: \mathcal{H} \rightarrow \mathcal{L}\) is the orthogonal projection onto \(\mathcal{L}\). \(\mathcal{L}\) is called a quantum error correcting code (QECC).
A large family of QECCs arises as stabilizer codes [5]. Let \(\mathcal{P}_n\) be the Pauli group on \(n\) qubits and \(S \subset \mathcal{P}_n\) be an Abelian subgroup that does not contain \(-I\). We define the logical subspace as
\[V_{S}:=\{|\psi\rangle \in \mathbb{C}^{2^{n}}|P| \psi\rangle = |\psi\rangle, \ \forall P \in S\}.\]
If \(S\) has \(n-k\) independent generators, the dimension of \(V_{S}\) is \(2^{k}\). The distance \(d\) is the minimal number of Pauli operator components whose products act on \(V_{S}\) in a nontrivial manner. \(V_{S}\) is a QECC of type \([[n, k, d]]\), which means that it encodes \(k\) logical qubits in \(n\) physical qubits and has distance \(d\). Using the error correction condition, we can show that such a code corrects arbitrary errors on \(\left\lfloor\frac{d-1}{2}\right\rfloor\) qubits. The Shor code [10]—which was the first QECC—is a \([[9,1,3]]\) stabilizer code whose stabilizer \(S\) is generated by check operators
\[Z_{1} Z_{2}, \ Z_{2} Z_{3}, \ Z_{4} Z_{5}, \ Z_{5} Z_{6}, \ Z_{7} Z_{8}, \ Z_{8} Z_{9}, \ X_{1} X_{2} X_{3} X_{4} X_{5} X_{6}, \ X_{4} X_{5} X_{6} X_{7} X_{8} X_{9}.\]
\(V_{S}\) thus has the following basis:
\[\begin{aligned}
|0\rangle_{L} & :=\frac{1}{2 \sqrt{2}}(|000\rangle+|111\rangle)(|000\rangle+|111\rangle)(|000\rangle+|111\rangle), \\
|1\rangle_{L} & :=\frac{1}{2 \sqrt{2}}(|000\rangle-|111\rangle)(|000\rangle-|111\rangle)(|000\rangle-|111\rangle).
\end{aligned}\]
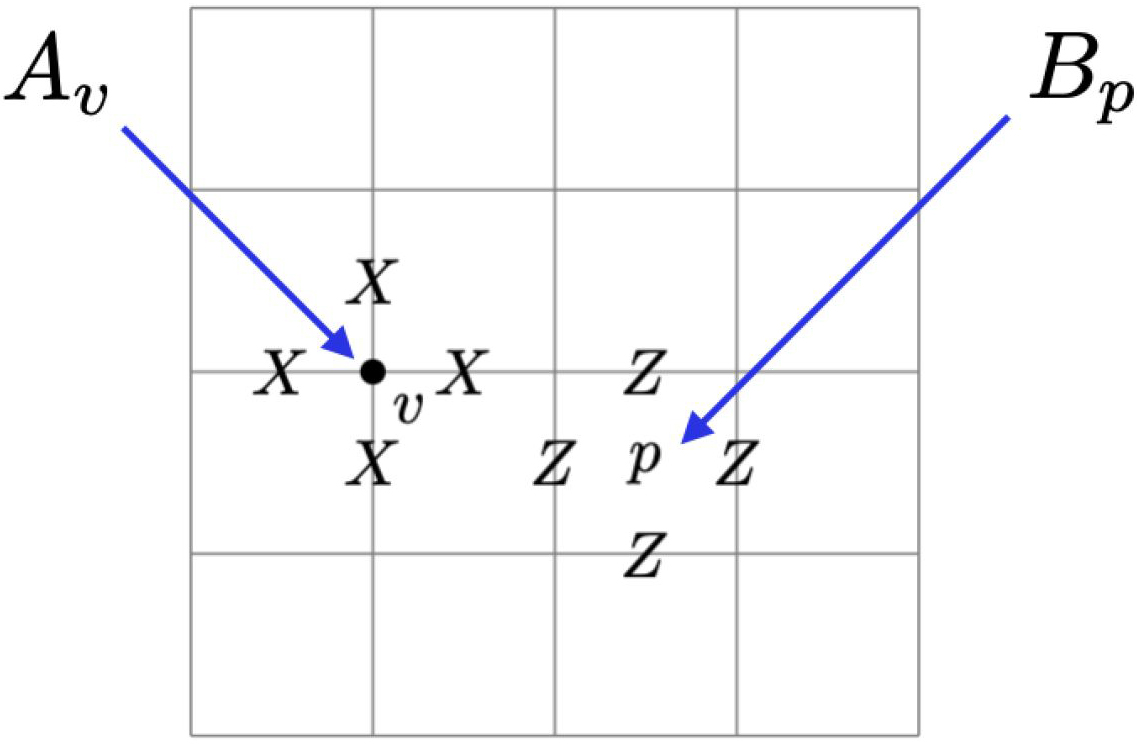
Another well-known QECC is the toric code [8]. Figure 1 depicts a square lattice wherein a physical qubit lives on each edge. The stabilizer consists of two types of check operators: \(A_{v}\) for each vertex \(v\) and \(B_{p}\) for each square \(p\). For a square lattice of size \(L \times L\) with a periodic boundary condition, the toric code is of type \(\left[\left[2 L^{2}, 2, L\right]\right]\).
Given a QECC that corrects errors on \(m\) qubits, consider a stochastic error model where—at each discrete time—an error occurs independently at every qubit with probability \(p\). The error correction process is successful as long as no errors spread more than \(m\) qubits; otherwise, a logical error is produced. We should therefore perform the correction process frequently and periodically to suppress the likelihood of errors on more than \(m\) qubits. According to a fundamental theorem, a threshold \(p_{t h}\) exists so that as long as \(p<p_{t h}\), the probability of a logical error can be smaller than that of a physical error [1]. By nesting several layers of the QECC to suppress the logical error rate to be arbitrarily small, we can achieve fault-tolerant quantum computing.
An important class of stabilizer codes is the low-density parity check (LDPC) codes (e.g., toric code), where each qubit participates in a constant number of check operators and each check operator comprises a constant number of qubits [6]. An active area of research involves seeking the ranges of parameters \([[n, k, d]]\) that a QECC can realize. We might also wish to optimize certain parameters over others, such as the encoding rate \(k / n\), distance \(d\), or threshold \(p_{t h}\). The toric code has a distance that scales as \(\sqrt{n}\). For a long time, scientists believed that the distance in an LDPC code was bounded by \(\operatorname{polylog} (n) \sqrt{n}\). But since 2020, researchers have broken this barrier with several methods, including the Hastings-Haah-O’Donnell fiber bundle codes with \(d \in \Omega\left(n^{3 / 5} / \operatorname{polylog}(n)\right)\) [7] and the Panteleev-Kalachev lifted product codes with \(d \in \Omega\left(n^{1-\alpha / 2} / \log (n)\right)\) for \(0 \leq \alpha<1\), which achieve almost linear distance [9]. Although the toric code has a very poor encoding rate of \(2 / n\), the utilization of tessellations on hyperbolic manifolds can achieve a constant linear encoding rate, even approaching \(1\) asymptotically.
The actual value of the threshold depends on the assumed error model and can reach as high as \(10^{-2}\) in the toric code [3] (compared to \(10^{-7}\) to \(10^{-3}\) for most other codes’ thresholds). LDPC codes are particularly useful in the current noisy intermediate-scale quantum era, when the number of physical qubits in a device ranges from \(10^{2}\) to \(10^{4}\) and the layout suffers from limited interconnectivity. It is challenging to design a code that optimizes more than one parameter and is simultaneously suitable for hardware implementation. Nevertheless, a recent collaborative project yielded some LDPC codes that outperformed toric code in encoding rate, had a high threshold when compared to toric code, and were potentially implementable on superconducting qubit-based quantum computers [2].
Finally, we will briefly mention another method that uses “hardware” to correct errors. Toric code can encode two logical qubits regardless of the lattice size because it represents a two-dimensional topological phase matter (TPM): a gapped quantum spin liquid that hosts quasiparticle excitations (also known as anyons). Anyons have a stable degenerate ground space and global degrees of freedom that local perturbations cannot access, which makes the multi-anyon space an ideal location for logical qubit storage. Logical gates, which are realized via the movement of anyons relative to each other, only depend on the isotopy class of the anyons’ worldlines. Essentially, the TPM itself is a QECC and error correction occurs at the hardware level. This innovative approach to fault tolerance is called topological quantum computing [4, 8]. Though it is a beautiful theory, experimental confirmation of the existence of anyons—especially those that are essential to topological quantum computing—is an extremely difficult task, albeit with high payoffs.
References
[1] Aharonov, D., & Ben-Or, M. (1997). Fault-tolerant quantum computation with constant error. In STOC ’97: Proceedings of the twenty-ninth annual ACM symposium on theory of computing (pp. 176-188). New York, NY: Association for Computing Machinery.
[2] Bravyi, S., Cross, A.W., Gambetta, J.M., Maslov, D., Rall, P., & Yoder, T.J. (2024). High-threshold and low-overhead fault-tolerant quantum memory. Nature, 627, 778-782.
[3] Fowler, A.G., Stephens, A.M., & Groszkowski, P. (2009). High-threshold universal quantum computation on the surface code. Phys. Rev. A, 80(5), 052312.
[4] Freedman, M.H., Larsen, M., & Wang, Z. (2002). A modular functor which is universal for quantum computation. Commun. Math. Phys., 227, 605-622.
[5] Gottesman, D. (1996). Class of quantum error-correcting codes saturating the quantum Hamming bound. Phys. Rev. A, 54(3), 1862.
[6] Gottesman, D. (2014). Fault-tolerant quantum computation with constant overhead. Quantum Inf. Comput., 14(15-16), 1338-1372.
[7] Hastings, M.B., Haah, J., & O’Donnell, R. (2021). Fiber bundle codes: Breaking the \(n^{1/2} \operatorname{polylog} (n)\) barrier for quantum LDPC codes. In STOC 2021: Proceedings of the 53rd annual ACM SIGACT symposium on theory of computing (pp. 1276-1288). New York, NY: Association for Computing Machinery.
[8] Kitaev, A.Y. (2003). Fault-tolerant quantum computation by anyons. Ann. Phys., 303(1), 2-30.
[9] Panteleev, P., & Kalachev, G. (2021). Quantum LDPC codes with almost linear minimum distance. IEEE Trans. Inf. Theory, 68(1), 213-229.
[10] Shor, P.W. (1995). Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A, 52(4), R2493.
About the Author
Shawn X. Cui
Associate professor, Purdue University
Shawn X. Cui is an associate professor in the Department of Mathematics and Department of Physics and Astronomy at Purdue University. His research interests include quantum computing, topological quantum field theory, category theory, and low-dimensional topology.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



